號稱以太坊的 VPN，Aztec Network 一直在努力使通用的零知識交易盡可能容易的進行，而零知識密碼學的快速發展有助於這一過程的實現。在這篇文章中描述一種幫助達到這一目的的基本密碼學技術。本文源自Aztec Network 密碼工程師 Luke Edwards 所著《Proof Compression》，並由 DeFi 之道編譯、整理。
（前情提要：Aztec是什麼，為何被FTX 警告封鎖？還有哪些混幣產品要小心？ ）
（背景補充：【Aztec Connect】 兼具隱私的擴容方案 —— 物理學徒專欄）
證明系統設計中需要權衡考慮的因素
在一個零知識證明系統中，當兩方相互接觸時，一方需要能夠說服另一方相信某些陳述是真的。
這其中的一方，我們稱之為證明者，而證明者希望說服的另一方，就叫做驗證者，證明者和驗證者之間擁有某種特定的訊息，同時他們要盡可能少的去分享這些訊息。這一過程通常可以簡單的分解為兩個階段：證明生成和證明驗證。
在理想的情況下，這兩個階段應該都是高速和高計算效率的，但現實是人們往往不得不對這兩個階段進行權衡。（在絕對的計算意義上，證明構建通常比驗證過程要更加昂貴，因此當我們談論例如「快速」的進行構建時，我們通常指的是相對於一些有意義的基準線更加快速，而不是相對於驗證過程更加快速）
在 Aztec 的零知識 rollup 的設置中，實際上有三個不同的方面參與到了 SNARK 證明的創建和驗證過程中，並且每個方面都有不同的計算能力和限制條件：
- 用戶：用戶擁有隱私訊息，如他們的餘額和他們的交易歷史，他們希望在參與交易和與 DeFi 協議的交互的過程中對這些訊息進行保密。他們會在網路瀏覽器中生成證明，這個過程通常是在手機等低功率設備上。
- rollup 提供者： rollup 提供者將用戶交易進行分批壓縮，這個過程涉及證明生成以及證明驗證，至少在某種意義上是這樣的（見下文關於遞歸的更多內容）。他們一般可以使用商業級別的硬體設施。
- 區塊鏈：以太坊虛擬機（EVM）是一個高度受限的計算環境，基於此的每個操作都有不同的成本，但通常很昂貴，並且必須由用戶來支付交易費用。以太坊虛擬機負責驗證一個證明（它封裝了許多其他證明）。
為了給 Aztec 的用戶帶來能負擔得起的、真正的零知識交易，我們將不同的證明系統（特別是 PlonK 的不同、美味的風味）跨越遞歸（recursion）的邊界融合在一起。對於用戶來說，這意味著他們在客戶端證明生成過程中減少了計算成本，以及通過將以太坊虛擬機的計算最小化來降低貨幣成本。
遞歸
遞歸基於的是以下強有力的觀察：零知識證明的驗證本身就是一個可以由零知識證明來證明的計算。
換句話說，沒有什麼可以阻止我們用一個證明 p* 來代替驗證一個 SNARK 證明 p 的行為，即 p 已經被正確驗證了。當然，通過這樣做，我們引入了 p*，它本身必須被驗證。但這從一開始就暗示了一個概念，即兩個不同的證明系統是如何被結合或「編寫（compose）」的。
讓我們把一個證明系統看作是一對算法（P，V），它代表一個證明者（P）和一個驗證者（V）。假設我們有一個證明系統（P，V），它有廉價的證明構造，但其證明驗證過程卻非常昂貴，還有一個證明系統（P*, V*），它有構造非常昂貴，但是驗證過程是廉價的。那有沒有一種方法可以將它們組合起來並獲得兩者的好處呢？請大家考慮以下過程：
- 在證明系統 P 下構建一個證明 𝛑。
- 在證明系統 P* 下構建證明 𝛑*，其中 p* 是證明 𝛑 在 V 下被正確驗證的證明。
- 驗證 𝛑*。
最終，這樣驗證的好處來自於這三個步驟中的每一步都可以由具有不同計算能力的各方來執行。通過這個想法延伸出的一個版本，正是使 Aztec Connect 能夠向其用戶提供廉價隱私交易的原因。而這裡所說的兩個證明系統就是 PlonK 和 TurboPlonK，前者有廉價的驗證，後者有高效的證明構造。我們在 rollup 中使用這種組合技術的簡化過程如下：
- 客戶端使用 TurboPlonK 來構建一個證明 𝛑-Client，這是一個帶有自定義門的 PlonK 變式（下面會有更多介紹），它允許在受限的設備上更高效的生成證明。它們將 𝛑-Client 發送到 rollup 提供者那裡。
- rollup 提供者隨後接收 𝛑-Client，並構建一個標準（即非 Turbo）PlonK 證明 𝛑-Rollup，其中證明 𝛑-Client 已經被正確驗證。從這個意義上來講，rollup 提供者一直受制於 TurboPlonK 驗證和標準 PlonK 證明構造的高成本。但是，rollup 提供者是強大的，它可以同時處理兩種證明系統，同時還可以賺錢並為用戶節省大量的資金。證明𝛑-Rollup最終被發送到以太坊上。
- 以太坊虛擬機通過部署到以太坊的智能合約 StandardVerifier.sol 來驗證 𝛑-Rollup。
注意：為了進一步優化壓縮過程，一個 Aztec 的 rollup 提供者實際上參與了三個遞歸步驟，兩個 Turbo-to-Turbo（使用 rollup 和根 rollup 線路，以這裡解釋的方式進行組裝）和一個 Turbo-to-Standard（根驗證器線路）。
自定義門（Custom Gates）
我們想通過一個假想的案例來說明 Turbo 和 Standard PlonK 之間的權衡問題。我們的目標是盡可能的將密碼學概念黑箱化，但我們要提醒讀者的是，下面的內容可能多少會有一點技術含量。
情景：你在一家名為 JazzTec 的公司擔任協議設計師。你設計並實現了一個名為 PlunK 的零知識證明系統，該系統允許用戶證明包括乘法和加法組合的語句，如 a+b=c，（a+b）-c=d，abc=d，等等。你的小型證明系統只包含一種門，它通過符號可以表述為：
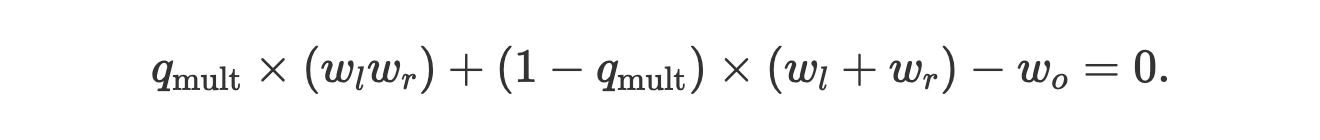
這裡的 w 代表「wire」，l = 左，r = 右，o = 輸出，q 是一個「選擇器（collector）」，用於在乘法和加法之間進行切換。JazzTec 的線路編寫員做了一個應用程式，用戶（或驗證者）必須證明他們已經找到了數位a、b、c 和 d，以便：
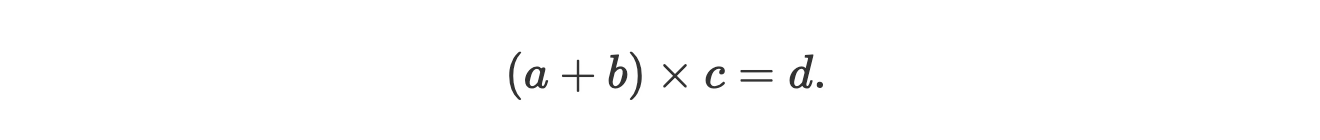線路編寫者為用戶提供了一個模板：
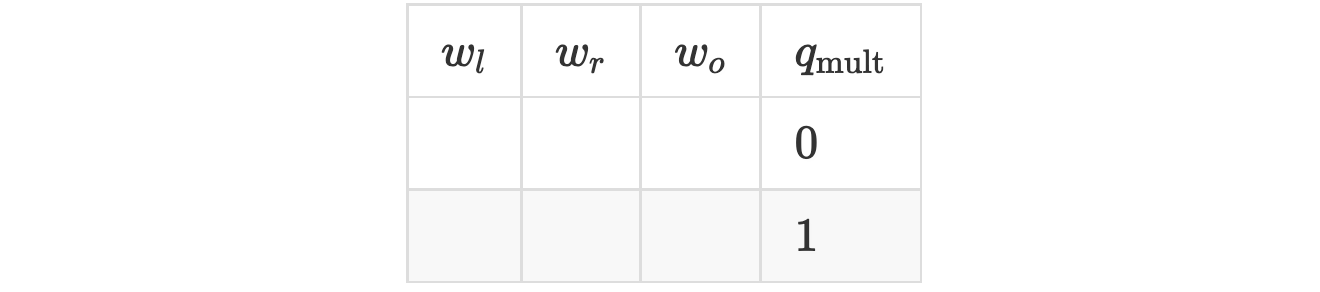
從原理上講，該線路看起來像是這樣的：
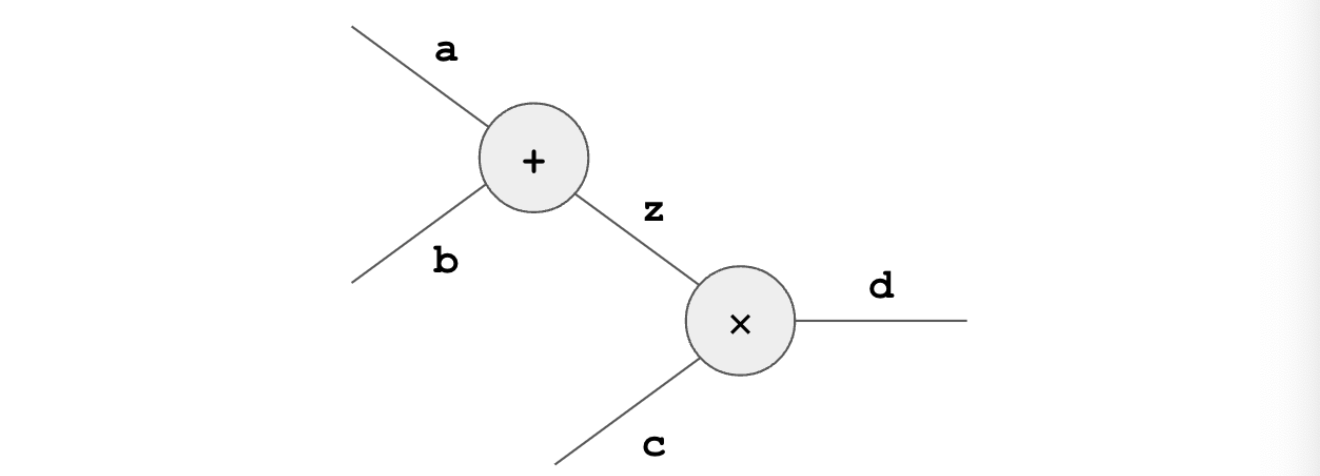通過在模板中填入 a、b、z、c 和 d 這些數值：
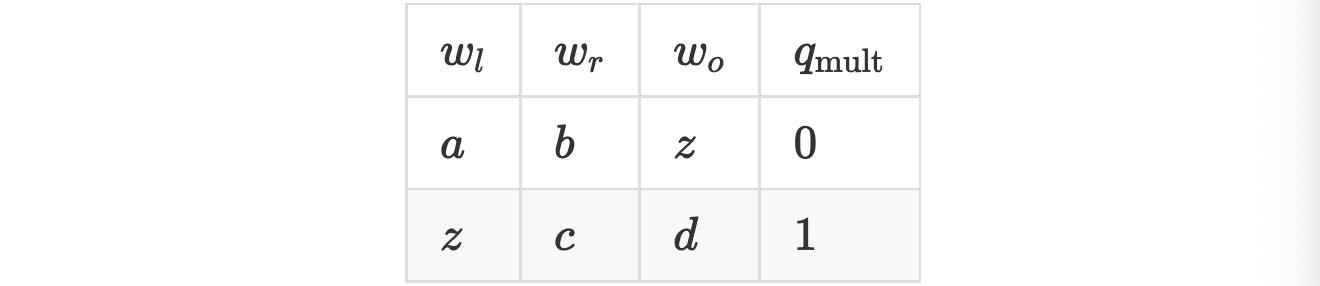用戶可以證明滿足要求數值的知識。（嗯，整個過程幾乎就是這樣的。我們忽略了一個事實，即 z 的兩個實例之間是必須是有連接的。這與複製限制條件的概念有關，這一點通常是非常重要的，但對於我們現在的觀點來可有可無）。
在使用 PlunK 一段時間後，JazzTec 決定增加一個新的功能，該功能要求用戶證明 x⁵=y 這樣的語句。（例如，最近開發的專門為零知識證明系統設計的 Poseidon Hash ，它需要進行五次冪的計算）。那麼我們該如何使用 PlunK 實現這種類型的操作呢？我們的表達式可以分解為一系列的乘法和一個加法，即：
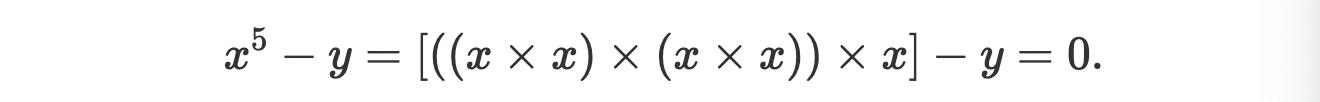
因此，為了處理這種操作而設計的線路部分可能看起來像是這樣的：
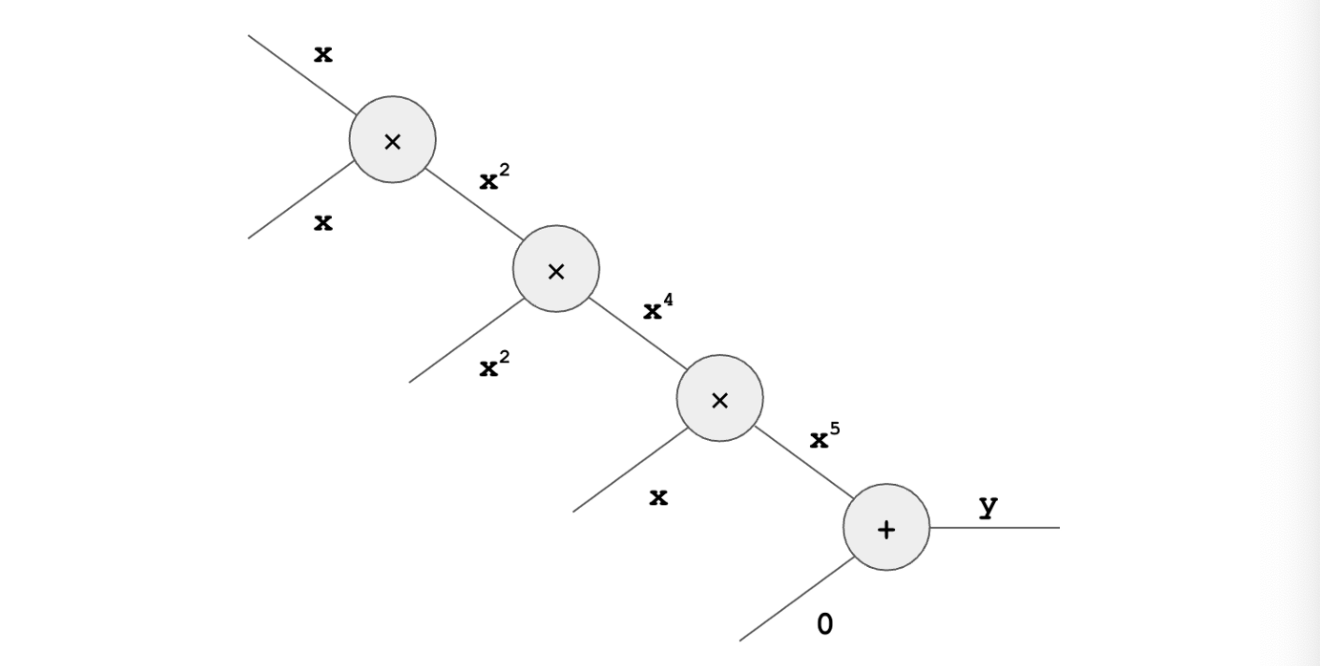
將這個新的組件添加到線路模板中後，其執行軌跡可以是這樣的：
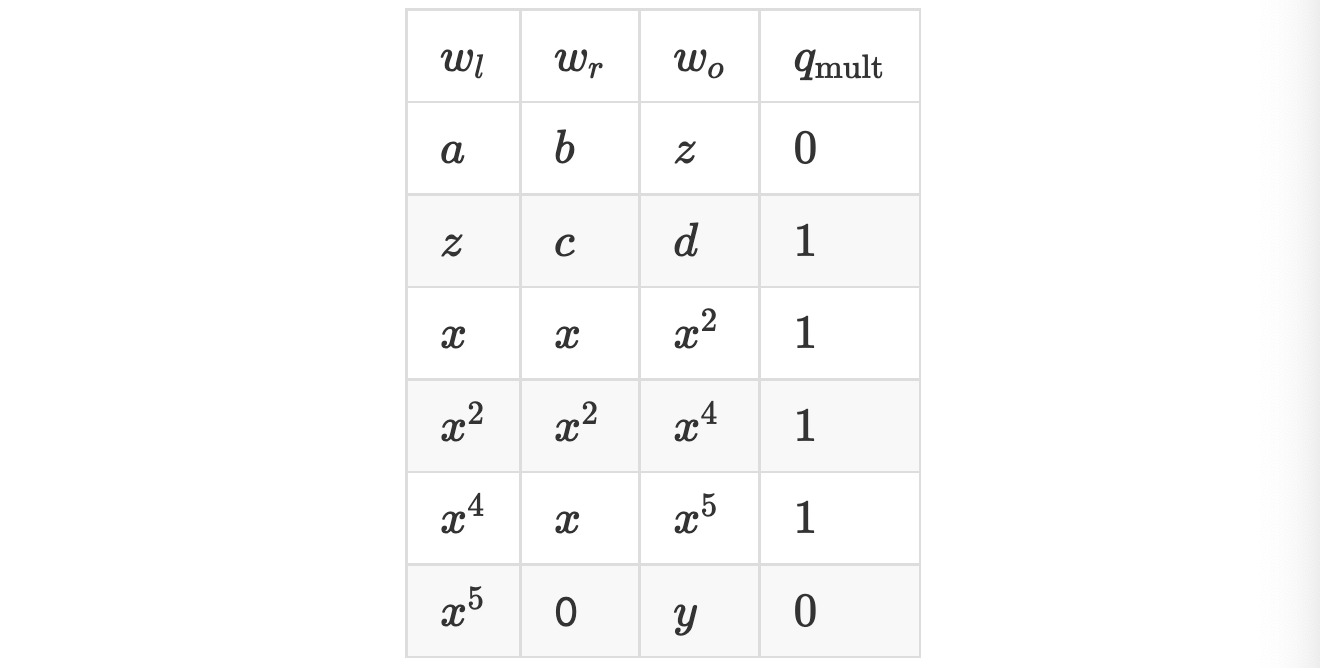
現在我們來考慮另一種方法。如果我們不使用 PlunK 的更簡單的設置，而是將證明系統擴展為一個對 x⁵=y 形式的語句提供本地支援的系統，那麼情況會如何呢？這裡的關鍵思想是，線路編寫者向驗證者指示要證明的語句的形式，並且可以添加一個新的選擇器，為執行軌跡中的每一行引入額外的解釋。
我們將把這種新的、擴展的證明系統稱為 TangoPlunK。它包含一個新的自定義選擇器，其通用門（generic gate）的形式為：
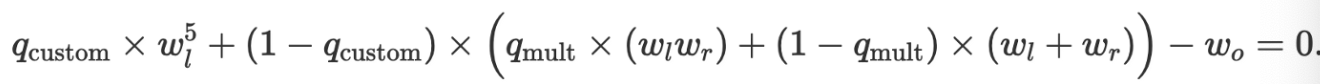我們看到，新的 q-custom 選擇器可以開啟或關閉自定義功能；當 q-custom 為 1 時，我們就有了五次冪方程，而當 q-custom 為 0 時，我們就有了舊的標準 PlunK 方程。現在，x⁵=y 所涉及的操作可以被封裝到一個單一的門中，它看起來像是這樣：
通過使用TangoPlunK，我們程式的執行軌跡就會變成了這樣：
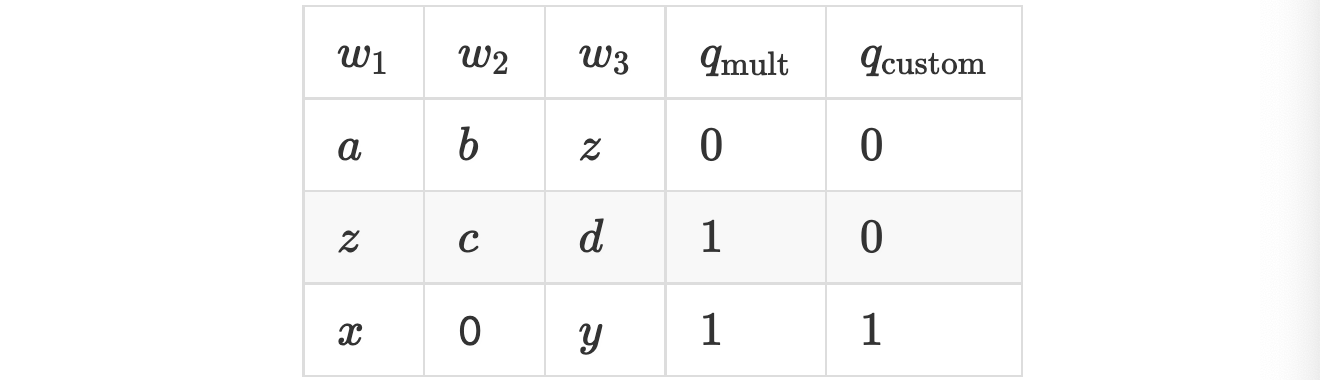
總而言之，以前完成整個驗證過程需要 6 個門，而現在就只需要 3 個，所以我們通過改用 TangoPlunK，將原有線路的複雜度減少了 50%！
對 TurboNerds 的一些補充
有經驗的讀者可能已經注意到了，為了處理五次冪類型的操作而引入的自定義門也增加了要證明的恆等式的程度。一般來說，這意味著驗證者的計算量將會增加，從而可能會抵消一些從減少線路大小中獲得的好處。
在我們上面的例子中，這相當於將恆等式的數量增加了一倍（從 PlunK 的 3 到 TangoPlunK 的 6），但是整個線路的大小卻減少了一半（巧合的是，它從 6 減少到了 3）。如果在我們的程式中可由定制門表示的計算比例較小，那麼我們就必須重新考慮其效用。在實踐中，這種權衡必須被考慮在內。
同樣重要的是，我們可以設想出一些有用的自定義門，它們不會增加恆等式的數量，或者至少不會讓驗證者感受到這種影響。例如，在最初的 TurboPlonK 證明系統中就是如此，其中關鍵的創新是引入了自定義門，它在計算 Pedersen Hash 的情況下促進了橢圓曲線標量乘法的有效進行。
證明者和驗證者的成本
我們以 PlunK 和 TangoPlunK 為例，旨在強調在設計證明系統時如何對於計算過程進行權衡，其依據是：（1）驗證器的複雜度從根本上與線路中的門數有關；（2）驗證器的複雜度與線路的大小相對獨立，但它會隨著被證明的要求或恆等式的複雜度而增加。
對於我們的樣本程式來說，TangoPlunK 的證明構造相對便宜，因為引入我們的定制門可以大大減少線路的大小。而在 TangoPlunk 中，驗證則是相對昂貴的，因為驗證者不僅看不到線路大小減少的好處，他們還必需面對一個相對於 PlunK 來說更加複雜的恆等式驗證。
更具體地說，在像 PlonK 這樣的證明系統中，驗證者和核查者的很大一部分計算成本是由於需要計算昂貴的橢圓曲線標量乘法而產生的。
對於驗證者來說，這些操作來自於在構建證明 𝛑 時需要計算的多項式承諾（commitment）。需要進行的標量乘法（scalar multiplication）的數量與被承諾的多項式的複雜性成正比，而這又與線路中門的數量成正比。（對於那些不熟悉多項式在 SNARKs 中所扮演的重要作用的人來說，我們建議你們閱讀 Vitalik Buterin 的這篇文章）
另一方面，對於驗證者來說，在使用 𝛑 中從證明方收到的承諾重構原始聲明或恆等式時，主要需要的是標量乘法。特別是在驗證過程中，恆等式中的額外選擇器會直接導致額外的標量乘法。例如，大家可以看一下標準 PlonK 驗證算法的第 9 步：
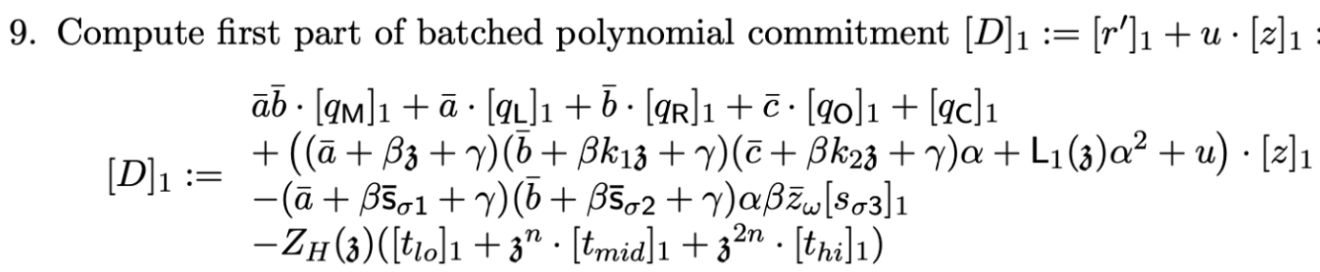這個表達式中的 q 是標準 PlonK 的選擇器，而運算符「·」代表橢圓曲線標量乘法。
上面給大家提供的例子說明了這種權衡：與標準 PlunK 相比，TangoPlunK 允許門的數量減少 50%，從而進一步降低了驗證器的成本（至少在承諾方面是這樣），同時也增加了驗證器的複雜性（通過增加選擇器 q-custom）。
當然，我們在這個例子中暗指的現實用例是標準 PlonK 證明系統和 TurboPlonK 之間的類似權衡。這就是為什麼在我們 Aztec 的應用中，比如 Aztec Connect，我們安排證明者使用 TurboPlonK，而驗證者使用的是 Standard PlonK。
進一步的探索
在過去幾年的事件裡，零知識密碼學已經出現了爆炸性的發展。在 Aztec，我們正在從 TurboPlonK 升級到我們所說的 UltraPlonK，它相當於是 TurboPlonK + Plookup ，這是我們設計的一個協議，用於使用查找表來進一步加快證明的構建，但驗證者則需要付出額外的成本。
在另一個極端情況下，我們設計了一個叫做 Fflonk 的協議，它允許在驗證者支付額外的成本的前提下進行極其有效的驗證。Fflonk 利用了這篇文章的承諾方案（我們稱之為 SHPLONK），它有可能將我們的以太坊虛擬機執行成本降低 35%。
結論
零知識證明是一個非常酷的、具有巨大技術潛力的前沿概念。我們在這裡所描述的技術是利用這種潛力來創造一個更好的網際網路的一小步。謝謝大家能加入我們的行列，並與我們一同前行。
感謝 Jon Wu、Ariel Gabizon、Suyash Bagad、Innokentii Sennovskii 和 Guillaume Drevon 對本文內容的積極評論和討論。
📍相關報導📍
OpenSea再添Optimism支援！上架Apetimism等NFT 、完善主要Layer2生態
觀點｜Layer2 賽道百花齊放、區塊鏈開啟戰國時代，誰將是領跑者？
【Aztec Connect】 兼具隱私的擴容方案 —— 物理學徒專欄
