假設區塊鏈在大規模的量子電腦攻擊下,是否能抵擋住其攻勢,本文將探討在量子電腦威脅下,區塊鏈可能面臨的挑戰以及應對方法。本文源自 BTQ 所著文章 《Blockchain security in the quantum era》,由 動區編輯部 整理。
(前情提要:淺析量子密碼學與加密技術:更強大的安全系統 )
(背景補充:量子物理專欄|談談「量子掏金熱」與泡沫 )
區塊鏈通常使用公開金鑰密碼系統(public-key cryptography),而現今大部分常用的系統皆建立在「整數因數分解(integer factorization)」和「離散對數問題(discrete logarithm problems)」這兩個數學問題之上,然而,在大規模的量子電腦攻擊之下,這兩者都會被破解。在此系列文章中,我們將探討在量子電腦威脅下可能的挑戰和應對的方法。
傳統電腦與量子電腦
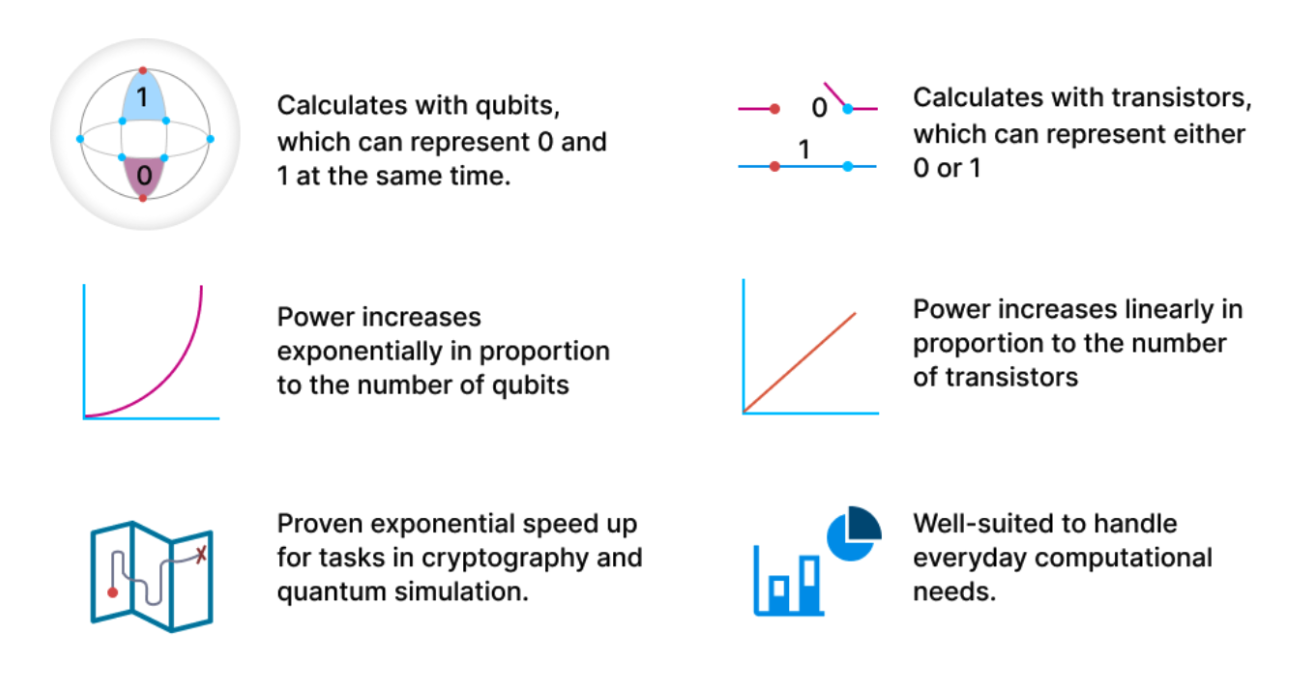
早在半個世紀前,我們就已經開始使用傳統電腦。從樹莓派到全世界最強大的超級電腦,我們所有的設備都是來自於古典電腦計算典範(classical computing paradigm),且這個計算典範是建立在二進位狀態之上。而量子電腦是一種迅速崛起的技術,其利用量子力學來解決傳統電腦難以解決的問題。
從計算的角度來說,傳統電腦和量子電腦的主要區別在於訊息處理的方式。傳統電腦將訊息儲存在二進位位元中,也就是每個位元只能處於兩種狀態中的一種(例如:開/關,高電壓/低電壓)。量子電腦將訊息儲存在量子位元(或稱量子比特, 即 qubits)中,訊息是以疊加態(superposition state)存在,每種狀態都有自己的機率幅(probability amplitude)。美國理論電腦科學家 Scott Aaronson 曾說:
「自然界不是由機率描述的(機率總是正數),而是可以由正數、負數或甚至是複數的振幅描述的。」
量子計算的特殊之處,就是在將機率理論推廣、允許負數,因為將兩個非零機率相加可以導致零機率,從而產生一種被稱為量子干涉的效應。多個量子位元群可以創造出高度複雜的多維空間,使得量子電腦能夠解決傳統電腦無法解決的問題。
何謂密碼系統中的「安全」?
我們通常使用以下兩種框架用來評估密碼系統的安全性:
- 計算安全(Computational security):假設對手沒有足夠的計算能力在合理的時間內破解密碼系統。
- 訊息論安全(Information-theoretic security):不假設任何有關計算能力的問題,而是透過數學證明其無法被破解。
然而,訊息論安全實際上非常難實現,所以大多數現代密碼協議都在對手的計算能力做了一定的假設。為了更好地理解計算安全框架中的這些假設,讓我們轉向計算複雜度理論來看看複雜度類別。
我們用 「P」表示可以在傳統電腦上有效解決的問題,「BQP」 表示可以在量子電腦上有效解決的問題,而 “NP” 表示可以在傳統電腦上有效驗證(但不一定可以解決)的問題。 過去數十年,許多電腦科學家和數學家對計算複雜度進行研究,並建立了密碼演算法之安全性分析的理論基礎,每個問題類別都由其是否可以被傳統電腦或量子電腦有效地解決或驗證來定義。現在,我們繼續討論這些複雜度類別與計算安全性的關聯。
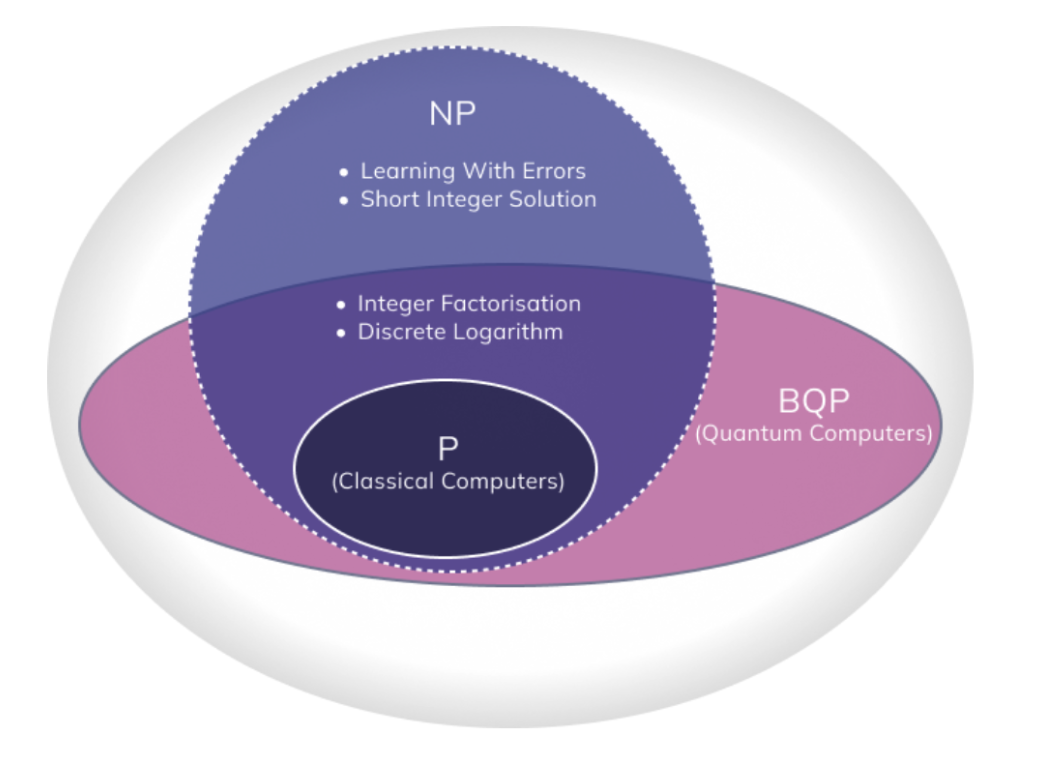
在 「P」中的問題已知可以由傳統電腦有效解決,無論是從計算安全或訊息論安全的角度,這些問題都不會有太多的幫助,因此如果要用來保護敏感資訊,我們會傾向選擇那些不在「P」中的問題。如果我們從 「NP」 的問題中選擇,可能仍然需要依賴計算能力上的假設,即我們假設對手不會在計算效率上有重大突破。所以,如果所選擇的問題不在 「P」中,但在 「BQP」 內,那麼這樣的演算法在量子時代可能會不安全,而這就是我們目前所處的情況。
在數十年前,當我們選擇各種難題作為密碼系統的假設時,我們選擇了不在 「P」中的難題,但從今日的觀點,這些難題仍在 「BQP」 內,這表示我們當時並不了解量子電腦的計算能力,或對「如何實現量子電腦」根本沒有頭緒,所以從當時的計算安全角度來看,這些難題依舊可以提供足夠的安全性。事實上,量子複雜度理論在 1992 年開始被提出,而 Shor 演算法(可有效破解橢圓曲線非對稱密碼系統的演算法)則是在 1994 年才出現的。意外的是,早在 1978 年,McEliece 就提出了一套非對稱密碼系統,它是基於一般線性錯誤更正碼的解碼困難度,此問題是 NP-hard,直至今日仍被認為不在 「BQP」 中,故能抵抗量子攻擊。
區塊鏈中的公鑰密碼系統
公鑰密碼系統是基於公鑰和私鑰的一對密鑰。密鑰對的生成是基於某些數學問題的難解性,因此私鑰計算出公鑰很容易,但反方向計算卻很難。公鑰會被傳送到區塊鏈上,私鑰則必須被保管起來,因為私鑰代表了區塊鏈地址的所有權和該地址所有資產的取得權。這種機制也形成了區塊鏈交易中至關重要的「數位簽章」。每個鏈上的交易都由私鑰簽署,以驗證發送者的合法性。簽署和驗證的流程如下:
- 簽署 (交易, 私鑰) -> 數位簽章
- 驗證 (交易, 公鑰, 數位簽章) -> 正確或錯誤
每一個區塊的每一個交易都需要進行數位簽章,而目前的數位簽章演算法大多基於 ECDLP(elliptic curve discrete logarithm problem,橢圓曲線離散對數問題)。ECDLP 已知可以被量子電腦有效解決,因此我們需要找到新的抗量子電腦攻擊的演算法。
量子攻擊如何破壞公鑰密碼系統
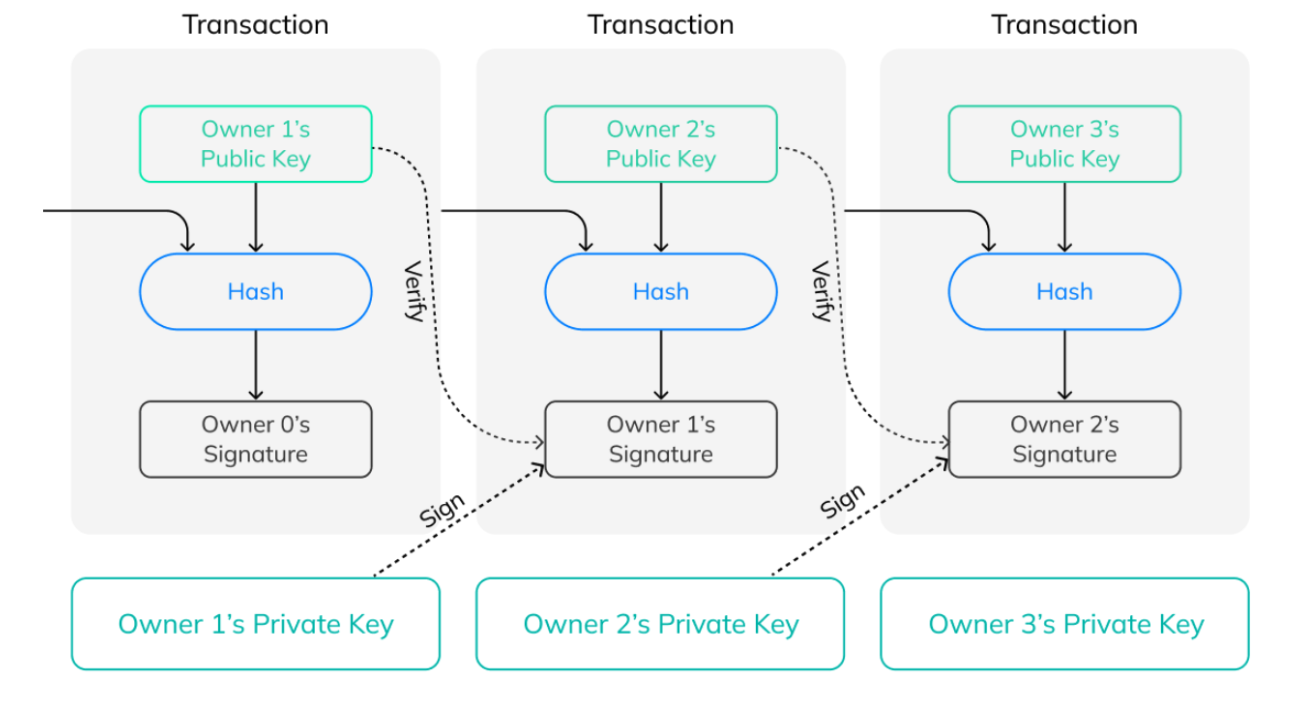
區塊鏈上的每個交易都需要使用私鑰簽署產生數位簽章,後由對應的公鑰來驗證交易的合法性。不幸的是,公鑰密碼系統的安全性是基於橢圓曲線離散對數問題(ECDLP)的困難度,而 Shor 演算法已提供了一個有效解決的量子演算法,也就是說,給定一組公鑰,一個夠強的量子電腦可以有效地計算出和它關聯的私鑰,如此公鑰密碼系統的遊戲規則將完全被破壞。典型的量子攻擊可能會經過以下過程:
- 為了從一個地址發送虛擬貨幣,必須揭露與該地址關聯的公鑰。
- 一旦公鑰被廣播,攻擊者就可以使用 Shor 演算法從公鑰中推導出私鑰。
- 利用推導出的私鑰,攻擊者就有能力創建交易,然後從該地址發送資產到其他地址。
區塊鏈的記帳方法大致分成兩種架構:UTXO(如比特幣區塊鏈) 和 Account-based(如以太坊)。簡單來說,前者比較像是現金交易,使用者可以同時從錢包動用多個錢堆進行交易;而後者比較像是銀行帳戶,一次只能進行一筆交易,交易完成才會進行下一筆。量子攻擊對於這兩種架構的影響如下:
- UTXO 架構:攻擊者可執行攻擊的時間比較短。在初次交易被確認並打包出塊之前,如果攻擊者能夠從被竊取的地址向自己的地址發送一個新的交易,那麼攻擊者就可能偷走所有屬於原始地址的資產。另外還有一些長期存在的地址,比如屬於交易所的地址,如果在接收客戶款項後不立即清空,亦有可能遭受到量子攻擊。
- Account-based 架構:攻擊者可執行攻擊的時間比較長。初次交易可能不會把所有的資產從帳戶中取走,即使初次交易發佈後,攻擊者仍可以繼續從帳戶中取走資產。
現在我們已經了解量子攻擊的原因、過程和結果,在下一篇文章中,我們將討論可抵抗量子攻擊的演算法。
下篇文章:BTQ研究》後量子時代的區塊鏈資安(下):更強的加密?淺談NIST後量子密碼標準
📍相關報導📍
深度|ConsenSys領軍的「Linea」:突破ZK Rollup限制、EVM完全相容





