很多市場可能沒有足夠的有機流動性來支持活躍交易。做市商就是解決這一問題的代理方,促使市場達成原本不會達成的交易。「自動做市商(AMM)」就是通過算法來實現這些功能的代理方,可以為數位化的市場注入流動性。本文源自於 Bollinger Investment Group 的 Dmitriy Berenzon 之文章《Constant Function Market Makers: DeFi’s “Zero to One” Innovation》,由專欄作者 以太坊愛好者編譯、撰寫及整理。
雖然自動做市商在理論和實踐上都有了長足發展,但是「常數函數做市商(constant function market maker,CFMM)」對學術界和金融市場來說是「從零到一」的創新。後者為數位資產交易所引入了確定性的定價規則,重新定義了做市商的流動性供給流程,並實現了全球資金池訪問平等化。
在這篇文章中,我將:
-
解釋 AMM 和 CFMM 之間的區別 -
探索 CFMM 的優缺點及其設計和用例的未來發展方向
術語解讀
儘管密碼學貨幣社群對自動做市商有濃厚的興趣,但是他們對相關術語的概念不甚了解。
每當談及自動做市商,大多數人都會想到 Uniswap 。實際上,過去十年來,已經有大量學術文獻研究了自動做市商這一概念。在大多數情況下,自動做市商主要是為了訊息聚合而設計的,並在收益取決於未來狀況的市場(例如,預測市場)中執行。
最受歡迎的自動做市商是 2002 年提出的對數市場評分規則(Logarithmic Market Scoring Rule)。大多數預測市場(例如,Augur 1.0 和 Gnosis )都採用這一模型。另外,用於訊息聚合的自動做市商模型種類繁多,例如,貝葉斯做市商(通常適合二元市場)和動態同註分彩做市商(常用於賽馬)。
雖然 Uniswap 確實是自動做市商,但是我們可以給出更具體的解釋。由於 Uniswap 做市商使用的是「常數乘積做市商」(詳見下文),我們將這類自動做市商歸入常數函數做市商一類。
每當談及 CFMM,人們經常會把它跟「聯合曲線(bonding curve)」聯繫起來,但這是不對的。聯合曲線定義了價格和代幣供應量之間的關係,而 CFMM 定義了兩個或以上代幣的關係。實際上,「聯合曲線」一詞的創造者指出,這個詞原本用於「聯合型策展社群」的語境中。
最後,經常有人將 Compound 等算法借貸協議稱作自動做市商。我相信,這些算法市場所使用的 AMM 是不包括 CFMM 的,因為利率函數是基於利用率的動態變化的,而且不以保持利率不變為目標。
延伸閱讀:新手介紹|如何在 DeFi 熱門項目「Uniswap」上賺取收益?
延伸閱讀:去中心化金融入門|五分鐘看懂借貸機制,什麼是「DeFi 銀行」Compound?
常數函數做市商
CFMM 是第一類應用於現實金融市場的 AMM 。密碼學貨幣社群設計 CFMM的目的是為了構建去中心化的數位資產交易所,並基於兩個或以上資產的可用數量在實際交易前預定義出一組價格(因為這種關係是根據函數確定出來的,相對價格會隨可用數量的改變而改變,邊買賣邊變)。不同於基於訂單簿的傳統交易所,交易者是基於一個資產池而非特定的交易對手進行交易。
「常數函數 」一詞指的是,無論交易如何改變資產儲備額,資產儲備額的乘積都是不變的(即,恆等於某個常數)。
-
交易者:使用一種資產交換成另一種資產 -
流動性提供者(Liquidity provider, LP):願意提供他們的資產組合來滿足交易需求,以此賺取交易費 -
套利者:將資產組合中資產維持在市場價格,並從中獲利
CFMM 通常用於二級市場交易,往往會通過套利交易準確反映每個資產在參考市場上的價格。例如,如果 CFMM 的價格低於參考市場價格,套利者會在 CFMM 上買入資產,然後到基於訂單簿的交易所賣出,以此獲利。
常數乘積做市商
常數乘積做市商由 Uniswap 率先實現。其公式如下所示:
![]()
其中,R(α) 和 R(β) 分別代表兩種資產的池內儲備數量,γ 代表的是交易費率。無論資產α或β的交易數量是多少,當費用為零時,R(α)*R(β)的乘積恆等於常數 k。這一等式常被簡化為 x*y=k,其中 x 和 y 分別代表兩種資產的儲備額。實際上,由於 Uniswap 會收取 0.3% 的交易費添加到資金池內,每筆交易都會增加 k 。
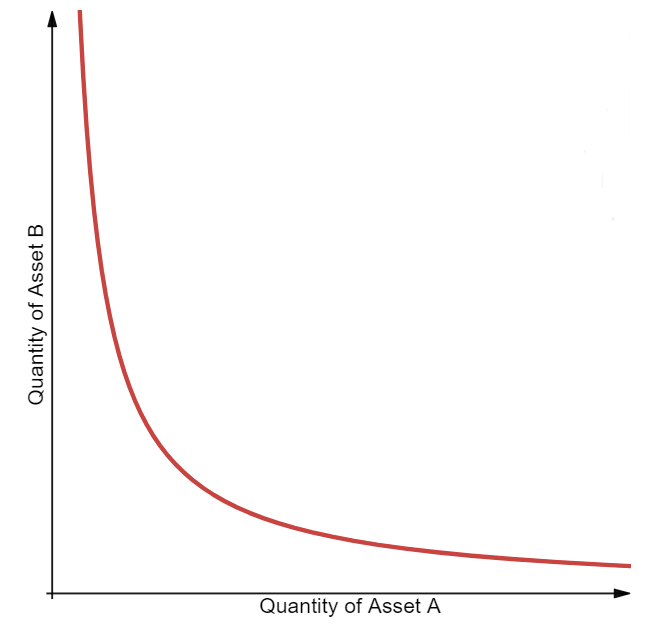
兩種資產的常數乘積函數構成一條雙曲線,其優點是資產價格越接近無窮大,越能產生流動性。
常數總和做市商
常數總和做市商是較為簡單的常數函數做市商的實現。其公式如下所示:
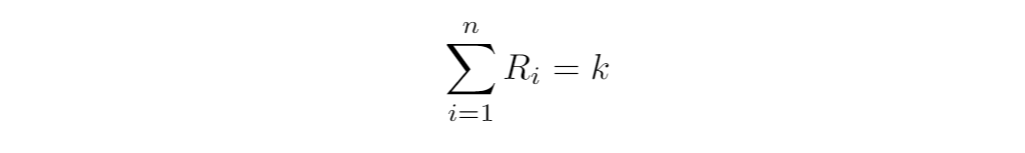
其中,R(i) 代表了每種資產的儲備量,k 是一個常數。儘管這個函數會產生「零滑點(zero slippage)」,但是它不能無限提供流動性,因此可能不適合作為獨立的去中心化交易所用例實現。實際上,如果作為儲備代幣的參考價格不等於 1 ,那麼所有套利者會不斷買入其中一種代幣,直至其流動性耗盡。
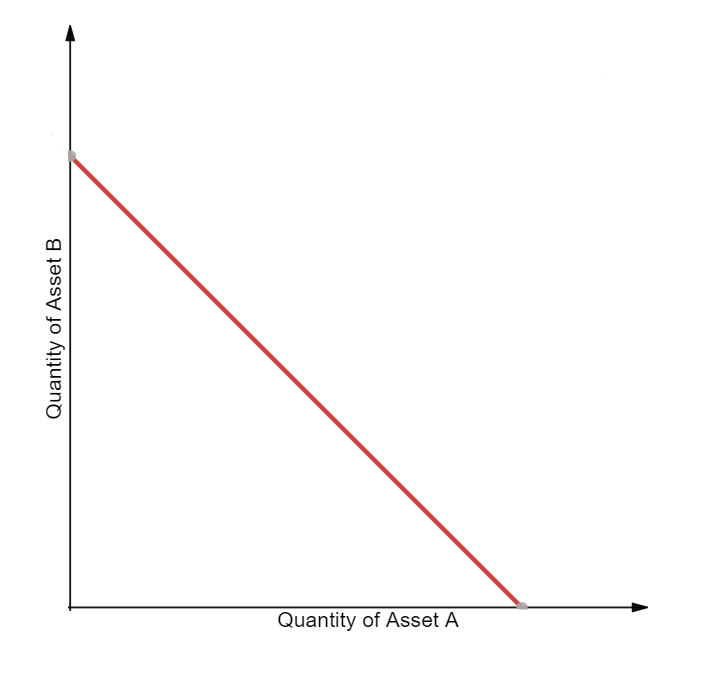
兩種資產的常數總和函數構成一條直線,並得到一個等式 x+y=k 。
常數平均值做市商
常數平均值做市商由常數乘積做市商這一概念推廣而來,可用於兩種以上資產,權重比例不僅限於 50/50 。常數平均值做市商由 Balancer 率先引入,其公式(不計入費用)如下所示:
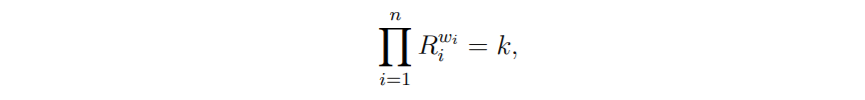
其中 R 代表每種資產的儲備量,W 代表每種資產的權重,k 是常數。換言之,在不計入費用的情況下,恆定平均值做市商可確保資產儲備量的加權幾何平均值保持不變。
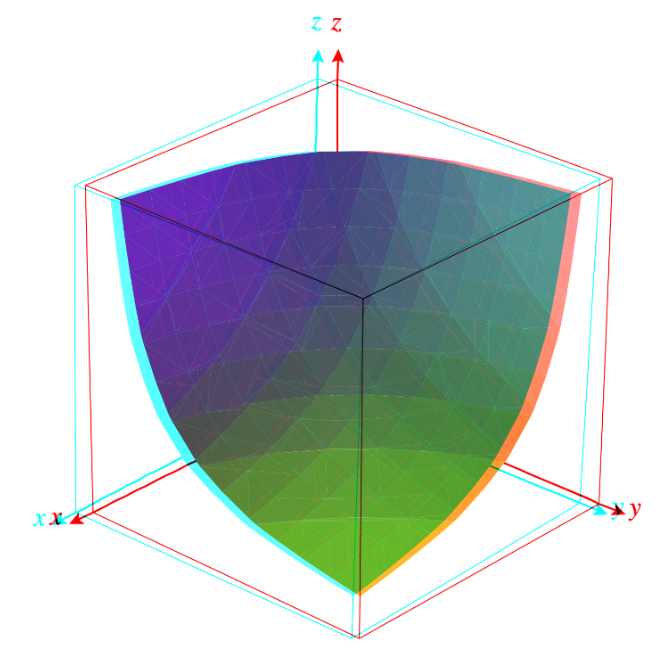
例如,三種資產的平均加權函數是 (x y z)^(1/3) = k 。
混合型 CFMM
一些項目根據交易資產的特徵使用混合函數獲得理想屬性。
Curve(又稱 Stableswap)的設想是,如果底層資產的價格相對穩定(例如,兩種錨定美元的穩定幣),就可以減少函數的滑點。因此,它採用了恆定常數和常數乘積的混合函數,得到了一個非常複雜的公式:
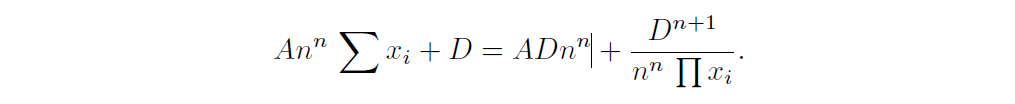
其中,x 代表每種資產的儲備量,n 代表資產種類數,D 代表儲備資產中的不變量,A 是「放大係數(這是一個可以調整的常數,會產生類似於槓桿的效應,並影響與流動性提供者收益相關的資產價格範圍,即,資產波動性越高,A 越高)」
當資產組合處於平衡狀態時,該函數就會發揮常數總和的作用,當資產組合的平衡狀態被打破時,該函數就會發揮常數乘積的作用。實際上,該函數看起來像是「放大的雙曲線」。
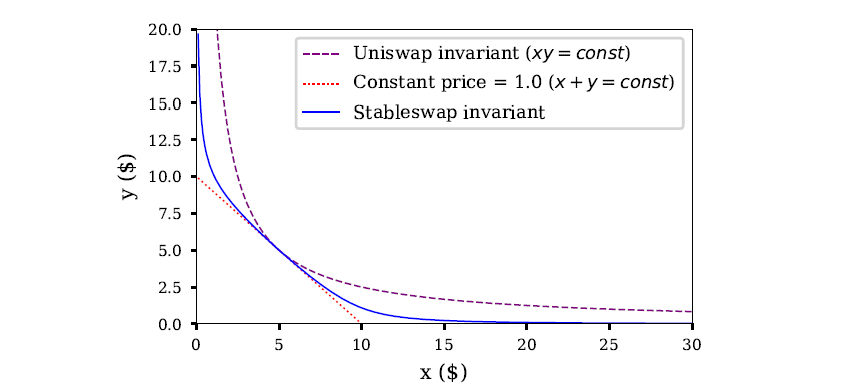
雖然 Shell Protocol 有著類似的目標,但是它採取的方法截然不同。它不僅像Curve 那樣利用穩定幣來優化函數的滑點,還像 Balancer 那樣使用加權資產籃子作為儲備資產,但是它的獨特之處在於,它引入了多個可調參數。其公式如下圖所示:
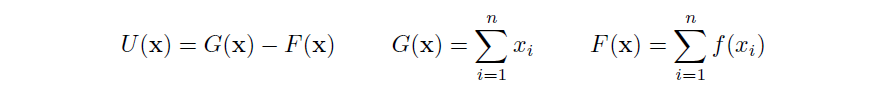
其中,U(x) 是由增益函數 G(x) 和損失函數 F(x) 組成的效用函數;x 代表的是每種資產的儲備量。實際上,當流動性池達到平衡時,該函數起到常數總和的作用,但是當流動性池中每種資產的權重都偏離指定閾值時,就會逐漸增加滑點。這種設計可以確保流動性池基於每種資產的預設權重保持平衡。
CFMM 的優勢
提高交易速度
在傳統的交易所流程中,做市商需要創建訂單,並將它們發佈到交易所上,然後瀏覽訂單,等待訂單成交。由於訂單需要被撮合,一些訂單可能需要等待較長時間才能成交。CFMM 可以解決經濟學上的「需求巧合( coincidence of wants)」 問題,讓交易立即達成,這一點對某些應用場景來說至關重要(例如,因流動性太低而難以造市的遊戲道具)。
引導流動性
對基於訂單簿的交易所來說,冷啟動流動性是一個非常複雜且成本高昂的過程。通常來說,交易所必須找到做市商,讓他們編寫自定義代碼來定價以及發布訂單,通常還要直接提供交易所需的帳戶和資金。交易所還要運行一個帶有控件的內部交易平台來執行一些交易,確保做市商不會通過搶先交易來損害客戶的利益。或者,交易所創始人會編寫一個 python 腳本,利用自己的資產來提供流動性,同時在其他交易所上對沖風險。對於「Delta neutral」 (譯者註:大意可理解為風險中性的,不偏愛也不厭惡風險)的做市商來說,很難找到一種方法來對沖帳面上資產,因為市場上沒有純粹的多頭或空頭。
由於 CFMM 鼓勵被動的市場參與者將資產借給流動性池,這種模式能夠大幅降低流動性供給的難度。例如,Synthetix 能夠使用 Uniswap 為其 sETH 流動性池引導流動性,讓用戶能夠更容易地在交易所上開展交易。
延伸閱讀:ETHFANS 專欄|DeFi 中的流動性和銀行擠兌風險,以 Compound 為例
鏈上訊息輸入系統
CFMM 無需通過中心化的第三方機構來衡量資產價格,從而解決了所謂的訊息輸入系統問題。受到經濟激勵的代理方在與 CFMM 交互時會提供正確的資產價格。因此,去中心化交易所成為了可靠的鏈上價格訊息輸入系統,可以作為智能合約的價格訊息來源。
Uniswap 2.0 又在此基礎上進行了完善,在每個區塊的第一筆交易執行之前確定並記錄價格,因此在出塊期間價格更難被操控。
路徑獨立
簡而言之,路徑依賴意味著「過往對未來有影響」。基於訂單簿的交易所的價格發現過程具有路徑依賴性,資產價格取決於參與者的行為反應。無論是在傳統市場還是中心化的密碼學貨幣交易所,這一點都很明顯,資產價格受到了訂單簿深度、買方或賣方流動性、交易歷史和私人訊息等因素的影響。
CFMM 具有很強的路徑獨立性(假設手續費率足夠低)。這意味著,任意兩種資產的價格取決於它們的數量,而非它們之間的路徑(曾經的歷史價格)。這會帶來兩大重要優勢:
-
無論交易者參與所有的交易,還是一小部分交易,得到的價格都是相同的。因此,交易者無需制定交易策略。 -
CFMM 通過了最小化的狀態表示:我們只需知道數量就可以對該資產進行定價。
CFMM 的劣勢
滑點
滑點指的是因交易者吸收流動性而導致價格與交易者行為背離的趨勢 —— 交易量越大,滑點越大。CFMM 會產生較高的滑點成本,因此適合體量較小的訂單。
外部金融風險
往 CFMM 中注入流動性雖然簡單,但是會帶來一些複雜的財務風險(暫時性虧損、短期波動性、長期波動性 / 交易量相關性等)。
例如,Uniswap 收益曲線的是凹形的。這意味著,流動性提供者在一定的價值範圍內是盈利的,在價格波動較大時會虧損。
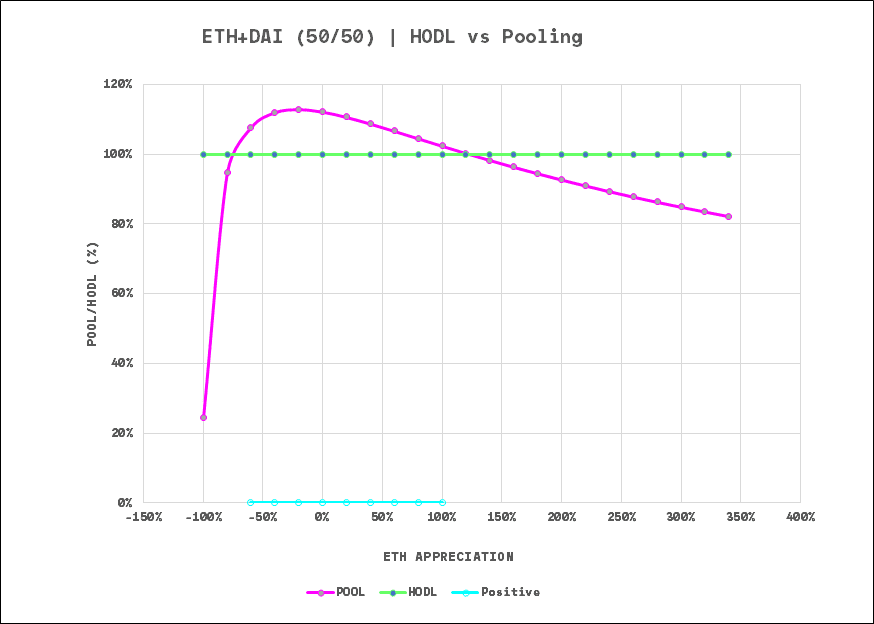
理想情況下,我們希望在承擔風險時,收益曲線呈「凸形」,也就是說,風險範圍的兩側都有上升空間。在這種收益結構下,流動性提供者應該積極監控流動性池的變化情況,並迅速採取措施來避免重大損失。
CFMM 的未來
特定資產函數
通過 Curve 和 Shell 的案例可以看出,我們可以針對特定類型的數位資產打造常數函數。
因此,我相信除了穩定幣之外,將會出現很多針對不同資產類型設計的 CFMM ,包括衍生品(例如,有擔保的期權)和證券性代幣(例如,房地產)。
這些 CFMM 的價格函數最能反映各類資產的特徵,從而減少滑點,並提升交易效率。
流動性敏感度
流動性敏感度的含義是,做市商會基於市場交易量來調整對定價反應的彈性。流動性敏感度是非常可取的,因為它在直觀上符合人們對市場運作的期望:同等資金規模的投入,在流動性充足的市場上比在缺乏流動性的市場上造成的影響更小。
目前,CFMM 模型的流動性敏感度受到價格的限制(即,流動性池越大,價格滑點越低),但是還有其他一些維度可以是動態的。
例如,固定的 LP 費用(流動性提供者費用)不具有流動性敏感度,因為該費用不隨交易量的變化而變化(即,無論流動性池的規模如何,費用始終保持在 0.3% )。
另一種方法是,在流動性較低時提高 LP 費用,來激勵流動性提供者存入資產(例如,當流動性低於一定的閾值時,費用會提高到 0.5% ,其他情況下維持在 0.3% )。
還有一種方法是,在市場誕生之初降低 LP 費用,以促進交易量,並隨著市場日趨成熟逐漸提高費用。雖然較低的 LP 費用會增加交易量,但是不利於聚集流動性。如何收取費用才能在平衡交易激勵與流動性激勵的同時實現收益最大化呢?這是個有趣的研究方向。
另外,LP 費用可以基於除流動性以外的其他因素。例如,人們可以根據拖尾波動性(trailing volatility)來調整 LP 費用,形成一種隨機定價機制,同時賦予 CFMM 「波動性敏感度」這一額外優點。
一級市場
雖然迄今為止大多數 CFMM 都用於二級市場交易,但是它們也可以用來引導一級市場的資產發行。通過 CFMM ,發行方可以提高實物資產和數位原生資產的發行效率,捕捉二級市場的上漲空間,並提高消費者的流動性和價格發現。
Unisocks 率先進行了嘗試。它創建了 $ SOCKS(襪子代幣),每個 $ SOCKS 都代表一雙限量版襪子。Uniswap 的 $ SOCKS/ETH 流動性池中有 500 $ SOCKS 和 35 ETH 。如果 ETH 的交易價格是 200 美元,則第一雙襪子的最低價為 14 美元,第 499 雙襪子的最低價約為 3.5 美元。Saint Fame 利用這一概念來售賣襯衫。Zora 更是利用這一概念創建了一個限量版市場。我希望未來看到更多項目使用 CFMM 發行代幣。
有趣的是,這又將我們帶回到了AMM 的初始用例,即,訊息誘導。但是,此時它影響的不是事件發生的可能性,而是資產的價格!
結論
CFMM 從根本上對金融市場進行了革新,並開拓了關於 AMM 的學術研究領域。
CFMM 仍處於發展初期。我期待未來幾年內會有新的設計和應用誕生。
?相關報導?
DeFi 新手科普 | 去中心化穩定幣 Dai 的十大應用場景
PeckShield 資安報告:4月共發生安全事件 15 起,DeFi 安全敲響產業警鐘
UX 大調查|DeFi 用戶人物誌:到底是哪些人在使用?
讓動區 Telegram 新聞頻道再次強大!!立即加入獲得第一手區塊鏈、加密貨幣新聞報導。
LINE 與 Messenger 不定期為大家服務









