以太坊顛覆了以太坊！「分佈式系統 + 密碼學」實現 2.0 性能突破

受困於分佈式系統 CAP 定理（不可能三角），公鏈要想改善性能是要付出代價的，當這個分佈式系統的用途是帳本時，這些代價甚至可能是難以被接受的。本文首發於安比實驗室。

本文目錄

以太坊也一直在嘗試各種方法以提升性能，在 2.0 被推出的前夜，它「試」出了密碼學。以太坊 2.0 將是一個以「分佈式系統+密碼學」為基礎來運轉的公鏈，這個密碼學不是指被用於簽名和隱私的那部分，而是指作為一個高性能系統的核心組件的那部分。

從這個角度而言，或許我們可以說顛覆以太坊的不是別人，而是它自己。它從分佈式系統設計的單一思路中跳了出來，走上分佈式系統+密碼學組合設計的道路。

這篇文章將試著介紹在以太坊 2.0 中，分佈式系統設計如何與密碼學設計結合，實現公鏈在性能上突破。

一、狀態分片：從單帳本到多帳本

區塊鏈是一個分佈式帳本，出塊節點是記帳的礦工，它們負責把交易寫入帳本。除了競爭記帳權，出塊節點最重要的工作，或者說本職工作就是檢查自己打包的這些交易是否合法。完成這個工作並不難，因為出塊節點手中握有帳本，它去查一下交易發送方有沒有這筆錢即可。

對於未分片的公鏈，所有節點都持有一個相同的帳本；而為了防止記帳衝突，每次也只允許一個出塊節點記帳。

以太坊提出狀態分片，實際上就是把一個帳本分成多個帳本，這樣一來，一些節點在 1 號帳本記帳，一些節點在 2 號帳本記帳……（相當於 7-11 從一個收銀台增加為多個收銀台），多個節點同時記帳，整個公鏈的性能就會得到質的提升。

但如果我們把出塊節點與帳本/分片的關係固定，比如確定由 a、b、c、d 四個節點負責 1 號帳本，那壞人只需收買 a、b、c、d 中的一部分就能破壞帳本，公鏈在提升性能的同時，安全性同比例下降。

因此，出塊節點需要被隨機、動態地分配到不同帳本，以此保證分片後的公鏈與未分片的公鏈具有相同的安全性。但動態分配會帶來新的問題：

節點手中該拿哪一個帳本？它可能會被分配到 64 個帳本（以太坊計劃啟動 64 個分片）中的任何一個去記帳。

以太坊給出的方案是出塊節點不拿任何一個帳本，或者說，讓出塊節點不需要帳本就能記帳。

這會帶來兩大好處，一是不管節點被分配到哪個分片，它都可以立刻開始記帳（出塊）工作，幾乎不用花費時間來獲得以及同步該分片的帳本，節點也因此可以在不同分片間輕鬆跳轉；
二是出塊節點不需要存儲帳本，也就不需要高硬件配置，任何人抵押32ETH就能成為一個驗證者，這非常有助於以太坊PoS的去中心化以及整個公鏈的安全。

但新問題躍然紙上：如果出塊節點手中沒有帳本，它怎麼知道交易發送方的錢夠不夠？

密碼學就在這時候登場了。

延伸閱讀：科普｜以太坊2.0 Staking 指南〈參〉：分片化的共識 Sharded Consensus

二、向量承諾：從查詢到證明

不需要帳本就能記帳聽上去不可思議，但其思路是簡單的：在以前，節點有帳本，一筆交易來後它翻看帳本，查詢交易是否合法；在以後，節點沒有帳本，交易發送方在提交交易的同時需要提交一個密碼學證明（為了區分，後文特指密碼學證明時都用 proof 表示），自己證明自己的這筆交易是合法的。

可出塊節點為什麼能夠通過一個 proof 來判斷某筆交易是否合法？這裡涉及到兩個密碼學的重要概念，第一個叫「成員證明」。

它指的是通過某種方法，證明個體是群體的一部分。如果能夠證明某個帳戶狀態是整個帳本狀態的一部分，出塊節點當然就能相信這個帳戶狀態，並以此為根據進行交易合法性的判斷。

第二個叫「向量承諾」。

它可以將群體，不管這個群體有多龐大，壓縮成僅僅一個數，然後給出成員證明，該成員證明表明的是某個個體是屬於這個數背後所關聯的群體的，且能證明個體在群體中的位置，以及進行證明的更新。

Merkle 樹是可被用於向量承諾的方法之一，我們以它為例來看如何實現成員證明。

下圖是一棵 Merkle 樹，最下一層的葉子節點存儲的是應用數據，其他非葉節點存儲的是其子節點的哈希值。如果知道綠色節點和所有黃色節點的值，就可以從下至上進行三次哈希運算，得到該 Merkle樹根的值，也就是 6c0a。

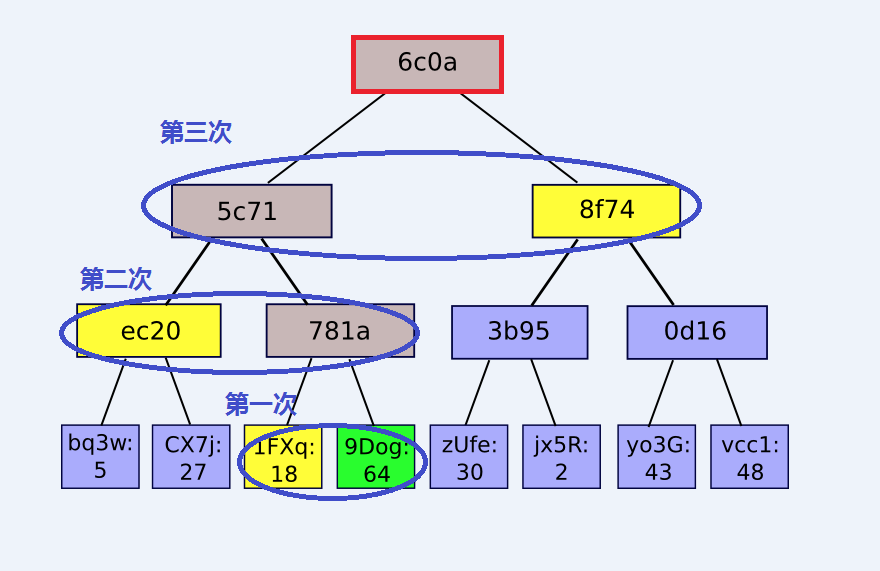
那麼，如果驗證方手中有樹根的值（6c0a），證明提供方把綠色節點的值和所有黃色節點的值作為一個 proof 給驗證方，驗證方是不是就能通過計算三次哈希的值是否等於 6c0a 來判斷綠色節點的值是否在這棵 Merkle 樹中？

答案是可以。這就是對綠色節點屬於 Merkle 樹的成員證明，它是以向量承諾的方式完成的，而這也幾乎就是比特幣 SPV 節點（簡單支付驗證）的工作方式。

延伸閱讀：閃電網路大進展！Lightning Lab 推出「無需帳密的」身份驗證協議

如下圖所示，SPV 節點不存儲完整的區塊/帳本，但存儲了每個區塊中 Merkle 樹的樹根（此Merkle樹的葉子節點存儲的是該區塊所有交易），當它需要查詢一筆交易是否存在時，會找全節點要一個該交易的 proof，該 proof 類似於上文中綠色節點和黃色節點值的一個打包（Merkle路徑），然後 SPV 節點會計算這些值的總的哈希值是否等於自己手中 Merkle 樹根的值，如果相等，則說明這筆交易是該Merkle樹的一個成員，即這筆交易是存在的。

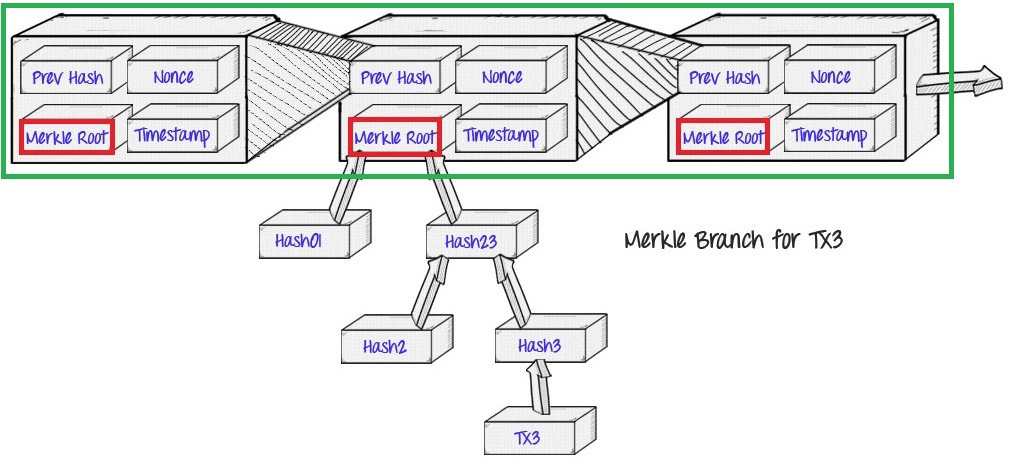
SPV 節點只存儲區塊頭（綠框），區塊頭中包含 Merkle 樹根（紅框）

SPV節點通過成員證明判斷交易是否存在，該證明系統包含三個部分：節點手中有一個簡短的摘要（樹根）；證明提供方給出一個 proof；節點計算此 proof，看是否與自己手中的摘要相符合。

到此，我們就完成了「不需要帳本就能查帳」，它是把查詢思路改為了證明思路；接下來我們要實現的是「不需要帳本就能記帳」。

對於以太坊 2.0 分片上的出塊節點而言，它的證明系統同樣是由摘要、證明、驗證這三部分構成，但它要做到是使用交易發送方（而不是全節點）給出的proof來判斷一筆新交易是否合法（而不是舊交易是否存在），並以此判斷為基礎記帳。

延伸閱讀：以太坊 Vitalik 回顧：區塊鏈 5 年前的 16 個問題都解決了嗎？

三、無狀態：從證明帳本到證明行為

想像有一個很小的村莊，這個村莊每天只有 3 筆村民間的交易，村長拿著帳本負責記帳。A 現在要給B 轉 5 塊錢，傳統的思路很簡單：村長看A 的帳戶上是否有 5 塊錢，如果有，就記下這筆新交易。

現在換一個思路：假設 A 在今天早上要給 B 轉 5 塊錢，村長知道 A 的帳戶在昨天早上有 10 塊錢，那麼如果 A 能夠證明昨天的 3 筆交易都和他沒有關係，是不是就意味著他的帳戶在今天早上依然有 10塊錢？這樣一來，村長是不是不用查帳本就能放心記下這筆新交易？答案是肯定的。

如果 A 昨天有一筆交易怎麼辦？很簡單，A 這時不是證明自己沒交易，而是證明自己昨天只有一筆交易，且那筆交易用掉了 3 塊錢；村長就知道他還有 7 塊錢，可以記下新交易。

這個思路的轉變至關重要，你一定要去理解它，這是「無狀態」這件事的奧妙所在。

不難發現，即使是不拿帳本的 SPV 節點，它在查詢交易時實際上也是要用到帳本，或者說狀態的，只不過它不是自己存儲狀態，而是去找全節點要這個狀態的證明；但在這個新思路下，狀態的作用可以徹底被「行為證明」取代，那麼這條鏈就能夠以無狀態的方式去設計。（注：行為證明這個詞並無出處，是作者為了易於理解這樣描述的）

如何實現無狀態？如何借助於行為證明完成記帳？依然是成員證明的方法。

延伸閱讀：巨大乾貨｜截至 2020 年 6 月，以太坊 2.0 發展狀況「全景式解讀」

能夠利用Merkle樹來完成這種成員證明嗎？理論上可以，但對於「無狀態」這個應用場景來說，用它的開銷過大。在本文中，我們將介紹通過「可聚合子向量承諾」來進行成員證明，以實現無帳本記帳。

可聚合子向量承諾（aSVC）是一個最新的研究成果，來自於論文《無狀態密碼貨幣的可聚合子向量承諾》，作者是Alin Tomescu、Ittai Abraham、Vitalik Buterin（以太坊）、Justin Drake（以太坊）、Dankrad Feist（以太坊）、 Dmitry Khovratovich（以太坊）。

其工作過程是這樣的：

1. 初始化分片

即在帳本建立時確定帳戶的初始情況。假設某個分片建立時有 100 個帳戶，這些帳戶都有初始的餘額，我們需要用 v(i) 代表第 i 個帳戶，它是（地址i，餘額i）這樣的一對值；用 V 代表全部帳戶，它是（地址1，餘額1）（地址2，餘額2）……（地址100，餘額100）這樣的一組值。

同時需要生成兩個值，第一個叫 c，它是對 V 的承諾，代表的是此時該分片所有帳戶和帳戶裡的餘額。出塊節點手中都握有 c，（可以對比 Merkle 樹根來便於理解），它是將來用於驗證的摘要。

第二個叫 π(i)，它是對 v(i) 是 V 的成員的證明，代表第 i 個帳戶及該帳戶的餘額是在總帳本 V 中。每個帳戶都握有且只握有自己的 π(i)，它是將來發送交易時提交給出塊節點的 proof。

在初始化階段，承諾和證明的生成是需要初始「狀態」的。

2. 第一筆交易

帳戶 i 發起整個分片的第一筆交易，此時它需要把 π(i) 和交易一起提交給出塊節點，出塊節點對 π(i)進行計算，看結果是否與自己手中的 c 相符合，如果一致就可以相信發送方帳戶確實有多少餘額，並以此判斷它提交的交易是否合法。

3. 關鍵：對 c 和 π(i) 進行更新

c（對整個帳本的承諾）不再是根據狀態生成，它是用第一筆交易發生之前的 c，以及第一筆交易引起的餘額變動生成的；π(i)（帳戶對自己的證明）也不是根據狀態生成，它是用第一筆交易發生之前的π(i)，以及第一筆交易對該帳戶的改變生成的。

在完成 c 和 π(i) 的更新之後，出塊節點手中便有了可以承諾所有用戶新餘額的新承諾（新c），帳戶手中也有了可以證明自己新余額的新proof（新π(i )）。

以此類推，每筆交易都會改變一次 c，改變一次全部 π(i)，但這種改變不再依賴於狀態數據，它取決於舊的 c 和 π(i)，以及上一筆交易；當需要驗證一筆新交易時，出塊節點手中總有最新的 c，它通過c和帳戶提供的 π(i) 就能判斷某筆交易是否合法，是否可被打包進區塊。

那麼到這一步，就終於實現了「不需要帳本就能記帳」，不管對於出塊節點，還是對於帳戶，它們手中握著的都是某種密碼學的證明，而不是帳本的狀態。另需一提的是，無狀態與分片似乎是絕配，但無狀態並不是針對分片的一種設計，它是針對公鏈的一種設計。

aSVC 的設計目標是要成為一個高效的成員證明，降低上述過程中的通信開銷和計算開銷，使得這種方案可用於無狀態區塊鏈的實現。從論文來看，使用 aSVC 方案，c 和 π(i) 的大小僅為幾十個字節，π(i) 的更新時間為 O(1)，驗證時間也為 O(1)，該方案還支持把多個 proof 聚合為一個 O(1) 大小的proof，這種低開銷的實現正是 aSVC 的意義所在。不過就像 Vitalik 在以太坊研究者論壇中展開的相關討論，aSVC 還需要做進一步的優化。

文章的最後是對全文的簡要總結：分佈式系統的狀態分片設計與密碼學的成員證明設計相結合，實現以太坊 2.0在性能上突破。

為了安全，以太坊 2.0 的狀態分片需要隨機分配出塊節點。
如果出塊節點需要帳本，帳本同步會成為新的性能瓶頸，帳本存儲也會影響 PoS 的去中心化
是否有不需要帳本就能驗證餘額的方式？
第一個思路轉變：把查找帳本的方式改為證明帳本的方式。這需要藉助於密碼學來完成。
第二個思路轉變：把證明帳本狀態的方式改為證明交易行為的方式，實現無狀態和無需帳本的記帳。這需要藉助於密碼學來完成。
密碼學的工具有很多，當有了目標後，需要根據應用需求選擇和組合適當的工具形成方案，並對方案進行優化。

延伸閱讀：以太坊 Layer 2 賽道解析：技術路徑權衡利弊後，哪些項目應該關注？

彩蛋、可聚合子向量承諾

在文章中我們用自然語言描述了 aSVC 的工作，如果你感興趣，可以通過 aSVC 的 API 定義來更清晰地了解它。如下圖所示：第一個紅框是初始化時生成承諾 c，第二個紅框是根據交易更新 c；第一個綠框是初始化時生成證明 π(i)，第二個綠框是根據交易更新 π(i)；藍框是出塊節點用 c 和 π(i) 做驗證。